Hi, In this post, we are going to review a short but interesting description of Bloom’s Taxonomy in Mathematics.

We shall start with the definition of bloom’s Taxonomy.

What is The Bloom’s Taxonomy?1

In 1956, Benjamin Bloom published a framework for categorizing educational goals: Taxonomy of Educational Objectives. Familiarly known as Bloom’s Taxonomy, this framework has been applied by instructors in their teaching 2.

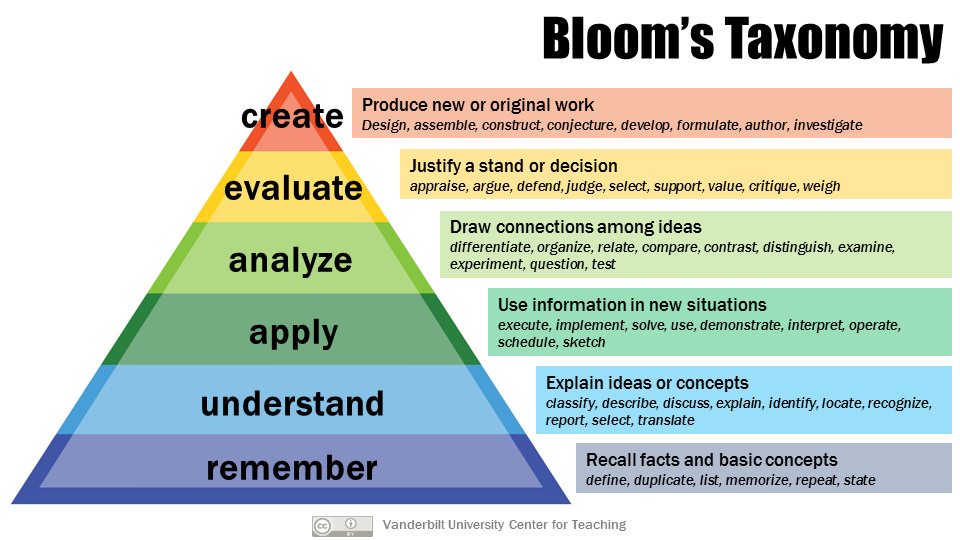
The framework elaborated by Bloom and his collaborators consisted of six major categories:

  • Knowledge => the recall of specifics and universals, the recall of methods and processes, or the recall of a pattern, structure, or setting.
  • Comprehension => a type of understanding or apprehension such that the individual knows what is being communicated and can make use of the material or idea being communicated without necessarily relating it to other material or seeing its fullest implications.
  • Application => use of abstractions in particular and concrete situations.”
  • Analysis => breakdown of a communication into its constituent elements or parts such that the relative hierarchy of ideas is made clear and/or the relations between ideas expressed are made explicit.
  • Synthesis => putting together elements and parts to form a whole.
  • Evaluation => judgments about the value of material and methods for given purposes.

A group of cognitive psychologists, curriculum theorists and instructional researchers, and testing and assessment specialists published in 2001 a revision of Bloom’s Taxonomy with the title “A Taxonomy for Teaching, Learning, and Assessment.”

This is revised taxonomy with the “action words”:

  1. Remember
    • Recognizing
    • Recalling
  2. Understand
    • Interpreting
    • Exemplifying
    • Classifying
    • Summarizing
    • Inferring
    • Comparing
    • Explaining
  3. Apply
    • Executing
    • Implementing
  4. Analyze
    • Differentiating
    • Organizing
    • Attributing
  5. Evaluate
    • Checking
    • Critiquing
  6. Create
    • Generating
    • Planning
    • Producing

If we know this taxonomy and categories, we can learn/teach efficiently and assess properly. We can use this anywhere we are learning, take the IELTS test as an example, and match the categories with steps of learning a new language.

Bloom's Taxonomy Pyramid
Bloom's Taxonomy Pyramid

What about Math?3

This is the same table from 3.

Level of Understanding Description Key Terms
Knowledge Questions involve stating definitions, theorems, steps to a given method, and other features of the course notes. List, define, describe, show, name, what, when, etc.
Comprehension “Use the definition to identify…”, “Which of the following satisfies the conditions of…”, “Use a specified method to…” Summarize, compare and contrast, estimate, discuss, etc.
Application Questions use more than one definition, theorem, and/or algorithm. Apply, calculate, complete, show, solve, modify, etc.
Analysis Questions require the student to identify the appropriate theorem and use it to arrive at the given conclusion or classification. Alternatively, these questions can provide a scenario and ask the student to generate a specific type of conclusion. Separate, arrange, classify, explain, etc.
Synthesis Questions are similar to Analysis questions, but the conclusion to be reached by the student is an algorithm for solving the given question. This also includes questions that ask the student to develop their own classification system. Integrate, modify, substitute, design, create, What if…, formulate, generalize, prepare, etc.
Evaluation Questions are similar to Synthesis questions, except the student is required to make judgments about which information should be used. Assess, rank, test, explain, discriminate, support, etc.

for example:

Level of Understanding Sample Question
Knowledge What are the conditions of the Mean Value Theorem.
Comprehension Find the slope of the tangent line to the following function at a given point.
Application Find the derivative of the following implicitly defined function. (This question might also involve logarithmic differentiation.)
Analysis Let f(x) be a fourth-degree polynomial. How many roots can f(x) have? Explain.
Synthesis Optimize the given quantity after generating the function that represents the given quantity.
Evaluation Related rate word problem where students decide which formulae are to be used and which of the given numbers are constants or instantaneous values.

The End.

  1. Armstrong, P. (2010). Bloom’s Taxonomy. Vanderbilt University Center for Teaching. Retrieved Sep. 6, 2021 from https://cft.vanderbilt.edu/guides-sub-pages/blooms-taxonomy/. ↩

  2. Wllingham, D. (2017). Bloom’s Taxonomy—That Pyramid is a Problem. Teach Like a Champion. Retrieved Sep. 6, 2021 from https://teachlikeachampion.com/blog/blooms-taxonomy-pyramid-problem/. ↩

  3. Shorser, L. (N.D.) Boom’s Taxonomy Interpreted for Mathematics. Department of Mathematics at the University of Toronto. Retrieved Sep. 6, 2021 from https://www.math.toronto.edu/writing/BloomsForMath.html. ↩ ↩2