Corona Product in Graph Theory
If you are interested in mathematics, you probably heard about graph theory and know what it is.
In this post, we considered our graph as a simple graph, which means there are no directed or multiple edges, and also, there is no loop in our graph.
You see a simple graph example below:
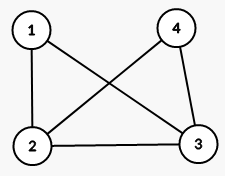
You should know that product operators are also defined in graph theory. There is plenty of definitions for product operator.
We are getting to know about one of these definitions, which is called “Corona Product”
Definition
Corona product of Graph G and H with $n$ and $m$ vertices respectively defines as follow:
\[G \odot H\]Note: the $G$ is on the left side of the operator, and $H$ is on the right side of it.
we create $G \odot H$ in two steps:
- First Step: Copy graph $H$, $n$ times ($|V(G)| = n$) and name them from $H_1$ to $H_n$ and put them around of graph $G$.
- Second Step: Connect all vertices of graph $H_i$ to one vertex in graph $G$. (for example suppose $ V(G) = \{ 1,2,…,n \} $ , so we connect all $H_1$’s vertices to 1 in Graph $G$, All vertices of $H_2$ to 2 in $G$ and so on. )
An Example
Let’s show you an example:
suppose:
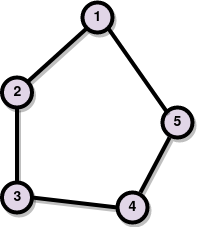
$ V(G) = \{ 1,2,3,4,5 \} $
$ E(G) = \{ \{1 , 2\}, \{2 , 3\}, \{3 , 4\}, \{4 , 5\}, \{5 , 1\} \} $

$ V(H) = \{ a,b \} $
$ E(H) = \{ \{a , b\} \} $
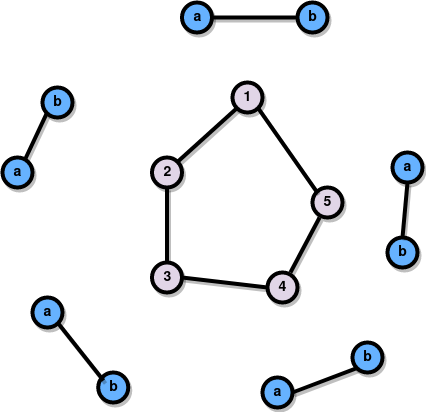
In the beginning, we copy the $H$, 5 times and spread them around the graph $G$:
Finally we connect vertices:
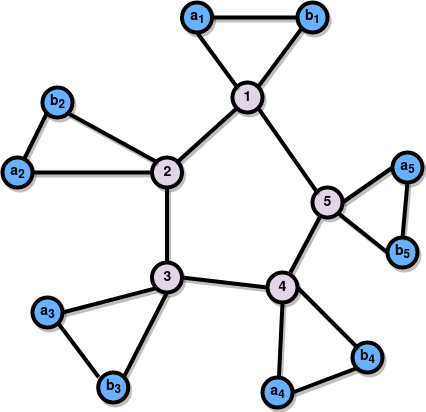
The last figure is Corona Product of two graphs, G and H.
You see?? It looks like a Coronavirus. In fact, corona means “something suggesting a crown” 1 :)
The end.
Enjoy Reading This Article?
Here are some more articles you might like to read next: