Recently, I attended the NeurIPS 2024 conference and encountered many fascinating papers and talks. Among these discussions, a recurring theme emerged: machine unlearning, particularly in the context of defining and quantifying unlearning.

To begin with, some papers argue that a certain degree of memorization is essential for models to generalize effectively 1 2. This is a compelling point, as memorization appears to play a critical role in enabling generalization. However, this raises an intriguing question: What happens if we attempt to unlearn that memorized data?

Consider a simple example that highlights the importance of memorization. While this example is straightforward and might not directly apply to the intricate architecture of a large language model or a complex neural network, it illustrates the concept well.

In a classifier like SVM (Support Vector Machine), the support vectors—data points close to the decision boundary—are crucial. We practically memorize these data to have the decision boundary 3. If we remove these support vectors, the decision boundary shifts, and the model’s ability to generalize diminishes significantly. This illustrates the idea that retaining certain memorized elements is essential for effective generalization. You can see the visualization of SVM classifier with different support vectors and different decision boundaries below (because of the different kernels, generated by this code):

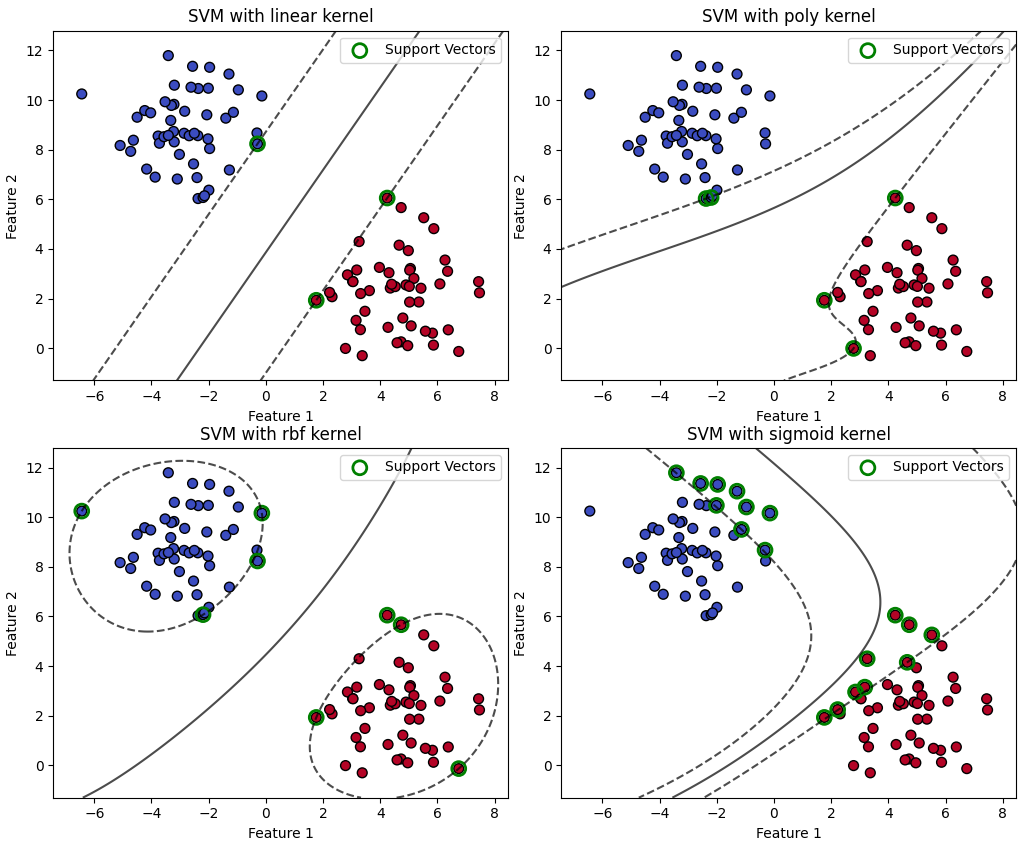
Support Vector Machine (SVM) visualization with decision boundary and support vectors for Poly, Linear, RBF, and Sigmoid kernels.
Support Vector Machine (SVM) visualization with decision boundary and support vectors for Poly, Linear, RBF, and Sigmoid kernels.

Additionally, knowledge itself is hierarchical and interconnected. For example, if I say I know linear algebra, it implies that I understand matrix multiplication, which in turn builds on a foundational understanding of scalar addition and multiplication. I cannot unlearn simple sum operations while retaining the ability to multiply matrices or the whole linear algebra knowledge.

This interconnected nature of knowledge leads to thought-provoking questions: Can I forget/change the sum operation while retaining more advanced concepts like matrix multiplication? Similarly, some types of knowledge, such as conclusions derived from a set of statements, are inherently complex. Can I unlearn the foundational statements while preserving the resulting conclusion?

These questions show that the unlearning is an interesting problem to work with and so many opportunities to have fundamental research.

– Ali

References

  1. The Privacy Onion Effect: Memorization is Relative ↩

  2. Does Learning Require Memorization? A Short Tale about a Long Tail ↩

  3. Support Vector Machine ↩